Introdução: O Número que Fascina a Humanidade
A sequência de Fibonacci e a proporção áurea representam um dos conceitos matemáticos mais fascinantes e onipresentes da história humana. Conhecida como φ (Phi), aproximadamente 1,61803398875, essa constante irracional aparece em contextos tão diversificados quanto a disposição das folhas em plantas, a estrutura de galáxias, obras de arte renascentistas, composições musicais e até no comportamento dos mercados financeiros. A relação entre Fibonacci e a proporção áurea é expressa matematicamente pela fórmula de Binet, que demonstra como os números de Fibonacci convergem para Phi. Este artigo explora as origens, fundamentos matemáticos e manifestações deste fenômeno universal.
Origens e Fundamentos Matemáticos
A Sequência de Fibonacci
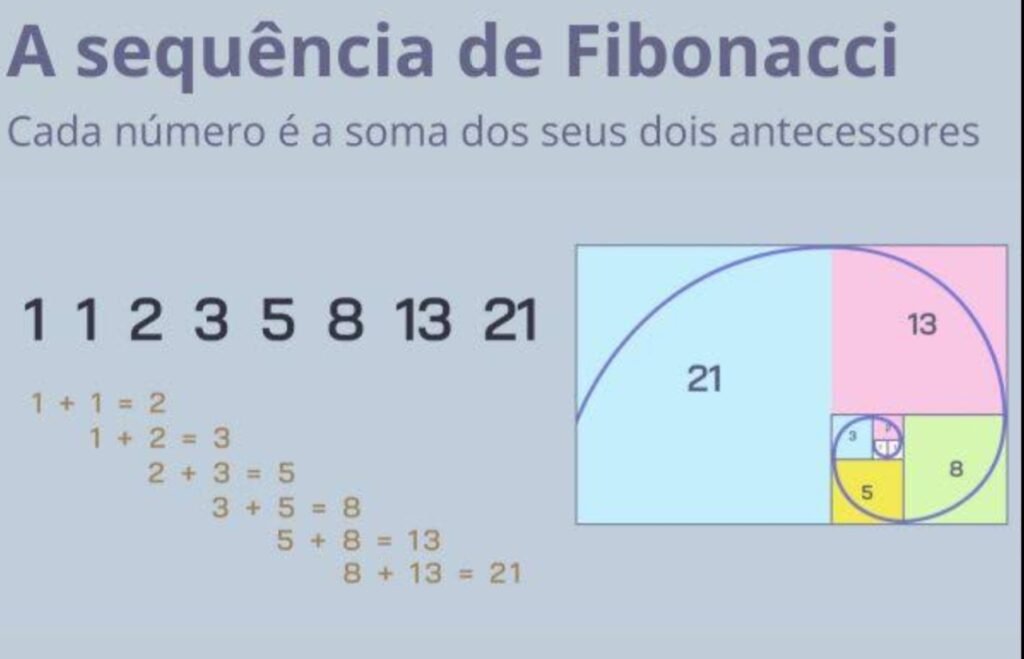
A sequência de Fibonacci é uma progressão numérica simples, porém profunda, onde cada termo subsequente é a soma dos dois anteriores:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, \ldots
Definida recursivamente por F_n = F_{n-1} + F_{n-2} , com F_0 = 0 e F_1 = 1 , ela foi popularizada no Ocidente por Leonardo de Pisa (Fibonacci) em seu livro Liber Abaci (1202), embora já fosse conhecida na matemática indiana séculos antes. Fibonacci a utilizou para modelar o crescimento idealizado de uma população de coelhos, assumindo condições biologicamente irreais, como reprodução perpétua e ausência de morte.
A Proporção Áurea (φ)
A proporção áurea surge quando uma linha é dividida em duas partes (a e b, onde a > b) tal que:
\frac{a + b}{a} = \frac{a}{b} = \phi
Algebricamente, φ é a solução positiva da equação quadrática:
\phi^2 = \phi + 1
que resulta em: \phi = \frac{1 + \sqrt{5}}{2} \approx 1,61803398875
. Uma propriedade notável é que seu inverso( \frac{1}{\phi} )) é igual a ( \phi – 1 \approx 0,618 , mantendo a mesma parte decimal.
Relação entre Fibonacci e φ
A conexão entre a sequência de Fibonacci e a proporção áurea é evidente ao se calcular a razão entre termos consecutivos:
\lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \phi
Por exemplo:
· \frac{2}{1} = 2
· \frac{3}{2} = 1,5
· \frac{5}{3} \approx 1,666
· \frac{8}{5} = 1,6
· \frac{89}{55} \approx 1,61818 . Quanto maiores os números,mais a razão se aproxima de φ. Essa relação é formalizada pela fórmula de Binet: F_n = \frac{\phi^n – (-\phi)^{-n}}{\sqrt{5}}
.
Manifestações na Natureza e Biologia
A proporção áurea e a sequência de Fibonacci aparecem prolificamente em sistemas naturais, frequentemente relacionados a padrões de crescimento e eficiência estrutural.
Botânica e Anatomia Vegetal
· Disposição de folhas (filotaxia): A organização das folhas ao longo de um caule frequentemente segue ângulos relacionados a φ (≈137,5°), maximizando a exposição à luz solar e ao fluxo de ar. Isso cria padrões espirais onde o número de espirais no sentido horário e anti-horário são números de Fibonacci consecutivos (por exemplo, 5 e 8, 8 e 13).
· Flores e frutos: O número de pétalas em muitas flores (lírios têm 3, margaridas 21 ou 34) e a organização das sementes em girassóis (89, 144 ou 233 espirais) refletem a sequência. No girassol, as sementes formam padrões espirais logarítmicos duplos, com números de Fibonacci, permitindo empacotamento eficiente.
· Estruturas de árvores: A ramificação de árvores e a disposição de galhos frequentemente seguem a sequência, com o número de ramos em cada nível correspondendo a termos de Fibonacci.
Zoologia e Anatomia Animal
· Conchas marinhas: A concha do náutilo exibe uma espiral logarítmica cujo fator de crescimento é φ. Cada nova câmara é aproximadamente 1,618 vezes maior que a anterior, uma adaptação que mantém a forma geométrica ideal durante o crescimento.
· Corpo humano: Proporções áureas aparecem em várias medidas anatômicas:
· A razão entre a altura total e a altura do umbigo até o chão.
· A relação entre o antebraço e a mão.
· A estrutura da face (distância entre olhos, largura do nariz, etc.), influenciando percepções de beleza e simetria.
· Estruturas microscópicas: O DNA possui 34 Å de comprimento por 21 Å de largura em cada ciclo completo da dupla hélice, ambos números de Fibonacci.
Astronomia e Física
· Galáxias espirais: Braços de galáxias como a Via Láctea formam espirais logarítmicas com fatores de crescimento próximos a φ.
· Sistema solar: As órbitas planetárias exibem relações baseadas em φ. Por exemplo, a razão entre os semi-eixos maiores de planetas consecutivos aproxima-se da proporção áurea.
Aplicações na Arte, Arquitetura e Design
Arte Renascentista e Clássica
Artistas e arquitetos têm usado conscientemente a proporção áurea para criar harmonia e beleza:
· Leonardo da Vinci: Em A Mona Lisa e O Homem Vitruviano, Da Vinci empregou retângulos áureos e proporções φ para definir composição e anatomia. No Homem Vitruviano, o umbigo divide o corpo na proporção áurea.
· Partenon de Atenas: A fachada deste templo grego se encaixa perfeitamente em um retângulo áureo, e várias de suas proporções estruturais refletem φ.
· Pirâmides de Gizé: A razão entre a altura original e metade do lado da base da Grande Pirâmide é aproximadamente φ.
· Obras modernas: Salvador Dalí (A Última Ceia) e Le Corbusier (módulos arquitetônicos) explicitamente incorporaram a proporção áurea.
Design e Arquitetura Contemporâneos
· Logotipos corporativos: Empresas como Apple, Twitter e Pepsi usam retângulos áureos e espirais para definir formas de logos, buscando apelo visual subliminar.
· Produtos de consumo: Cartões de crédito, telas de dispositivos e até embalagens frequentemente adotam proporções áureas para estética agradável.
Música: Estruturas Harmônicas e Composição
A música, como arte baseada em relações matemáticas, abunda em exemplos de φ.
Proporções em Instrumentos
· Violinos Stradivarius: As posições dos “f-holes” e as proporções do corpo refletem a proporção áurea, contribuindo para sua qualidade acústica excepcional.
· Piano: Uma oitava cromática compreende 13 teclas (8 brancas, 5 pretas), números de Fibonacci consecutivos. Acordes maiores são construídos sobre a terceira, quinta e oitava notas da escala, todas posições de Fibonacci.
Composições Musicais
· Estruturas formais: Muitos compositores dividem obras em seções cujas durações relacionam-se com φ. Por exemplo:
· Bartók: Music for Strings, Percussion and Celesta usa a sequência para determinar número de compassos e clímax.
· Debussy: Dialogue du vent et de la mer emprega proporções áureas na estruturação frasal.
· Mozart: Sonatas frequentemente dividem temas em subseções de 5 e 8 compassos.
· Frequências e harmonia: A razão entre frequências de intervalos musicais às vezes aproxima-se de φ (por exemplo, terça maior ≈ 1,25, não exatamente φ, mas compositores ajustam tempos e intensidades).
Mercado Financeiro: Retrações de Fibonacci
Na análise técnica de mercados financeiros, retrações de Fibonacci são ferramentas populares para identificar potenciais suportes e resistências.
Fundamentos da Análise
· Retrações: Após um movimento significativo de preços (alta ou baixa), traders traçam retrações dos níveis chave: 23,6%, 38,2%, 50%, 61,8% e 100%. Os níveis de 38,2% e 61,8% derivam diretamente de φ ( \frac{1}{\phi} \approx 0,618 e ( \frac{1}{\phi^2} \approx 0,382 )).
· Ondas de Elliott: A teoria postula que os mercados movem-se em padrões de 5 ondas de impulso e 3 de correção (um total de 8, outro número de Fibonacci), e que as relações entre altas e baixas frequentemente aproximam φ.
Aplicação Prática
· Exemplo em tendência de alta: Se um ativo sobe de R$ 100 (ponto A) para R$ 200 (ponto B), em seguida corrige, os traders esperam suporte próximo:
· Retração de 38,2%: R$ 200 – (R$ 100 × 0,382) = R$ 161,80
· Retração de 50%: R$ 150 (embora 50% não seja estritamente Fibonacci, é comumente usado)
· Retração de 61,8%: R$ 200 – (R$ 100 × 0,618) = R$ 138,20.
· Confirmação: Esses níveis ganham validade quando coincidem com outras ferramentas técnicas, como médias móveis ou linhas de tendência.
Eficácia e Críticas
Embora amplamente utilizadas, retrações de Fibonacci não são infalíveis. Críticos argumentam que se tornam profecias autorrealizáveis devido à adoção generalizada. No entanto, sua persistência sugere que capturam aspectos da psicologia de mercado e comportamento coletivo.
Curiosidades e Aspectos Adicionais
Propriedades Matemáticas Notáveis
· Expressões alternativas: φ pode ser representado como uma fração contínua simples:
\phi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}
e como um radical aninhado:
\phi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \ddots}}}}
].
· Relação com π e e: Existem identidades conectando φ com outras constantes fundamentais, como:
\phi = 2 \cos(\pi/5)
].
Cultura e Contexto Histórico
· Nomenclatura: O termo “proporção áurea” (golden ratio) foi cunhado por Martin Ohm em 1835, enquanto Luca Pacioli a chamou de “Divina Proportione” em 1509.
· Controvérsias: Algumas alegações de ocorrência da proporção áurea são exageradas ou apócrifas. Por exemplo, não há evidências sólidas de que os antigos egípcios conscientemente a usaram nas pirâmides.
Conclusão: A Matemática Universal
A sequência de Fibonacci e a proporção áurea transcendem disciplinas, aparecendo como um fio condutor matemático tecido através da natureza, arte, música e até finanças. Sua ubiquidade sugere que pode refletir princípios fundamentais de crescimento, eficiência e percepção estética inerentes ao nosso universo. Seja pela intenção consciente de artistas e arquitetos ou através de processos evolutivos cegos, φ emerge como uma constante de harmonia e equilíbrio. No entanto, é crucial abordar alegações com ceticismo científico, reconhecendo que a beleza da matemática está tanto em sua aplicação quanto em sua elegância abstrata.
Como Johannes Kepler refletiu, a geometria detém dois grandes tesouros: o teorema de Pitágoras e a divisão da linha em extrema e média razão. O primeiro é uma massa de ouro; o segundo, uma joia preciosa.
